Quantum error correction (QEC) is a cornerstone for building reliable quantum computers from noisy hardware. While standard approaches based on topological codes, such as surface and color codes, have achieved remarkable experimental progress, their low encoding rates typically require millions of physical qubits for practical applications. To overcome this bottleneck, interest is growing in quantum low-density parity-check (QLDPC) codes, which can in principle dramatically reduce the resource overhead of QEC. Among these, the bivariate-bicycle (BB) codes recently proposed by IBM have drawn particular attention, as they are expected to reduce resource demands by an order of magnitude while remaining compatible with near-term hardware [1].

Recently, a collaboration led by researchers from the Institute of Theoretical Physics, Chinese Academy of Sciences (Prof. Hao Song, Ph.D. student Keyang Chen, and M.S. student Yuanting Liu), the University of Science and Technology of China (Prof. Ke Liu and Ph.D. student Yiming Zhang), and Peking University (Prof. Yu-An Chen and Ph.D. student Zijian Liang) has made significant theoretical progress in this class of QEC codes. The team innovatively combined algebraic, geometric, and topological methods to establish a topological framework for studying BB codes. This work, titled “Anyon Theory and Topological Frustration of High-Efficiency Quantum Low-Density Parity-Check Codes,” was published in Physical Review Letters [2].

The main highlights of this study are as follows:

A “fracton” perspective helps establish the topological framework. The researchers observed a methodological analogy between BB codes and fracton physics—the study of exotic quasiparticle excitations that cannot move freely [3,4]. By adapting algebraic tools developed in the study of fractons [5] and combining them with methods such as Gröbner bases, they achieved an efficient characterization of the topological properties of any given BB code. The study reveals that such QEC codes generically possess topological order with anyonic excitations. However, these anyons exhibit some quasi-fractonic features, as their short-range movement is necessarily accompanied by a change in energy (Fig. 1).

“Topological frustration” is revealed to analyze the code space. The work further uncovered a phenomenon the researchers term “topological frustration.” Unlike conventional topological codes, the ground-state degeneracy of BB codes on a torus is typically smaller than the total number of anyon species. The study shows that this phenomenon is closely tied to the quasi-fractonic mobility of anyons, with both aspects reflecting a deeper structure known as translation symmetry-enriched topological order. By exploiting the symmetry properties of the Koszul complex, the researchers established a precise correspondence between logical operators and anyon excitations in the presence of topological frustration.

Algebraic geometry uncovers how topological order varies. Methodologically, beyond using Gröbner bases to characterize individual BB codes, the researchers innovatively employed algebraic geometry methods based on the Bernstein–Khovanskii–Kushnirenko (BKK) theorem. This approach revealed how the topological order of BB codes with near-toric-code layouts varies with their defining parameters. According to the BKK theorem, the total number of anyon types can be determined by computing the mixed volume of Newton polytopes specified by the interaction forms (in two dimensions, this reduces to the mixed area of Newton polygons, Fig. 1).

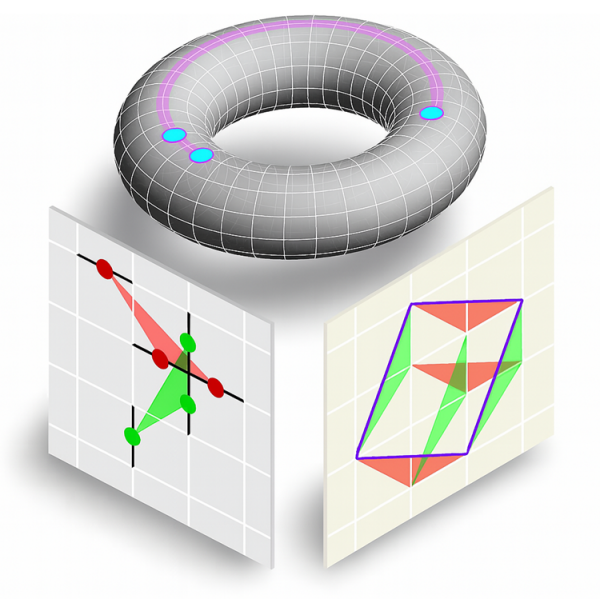
Figure 1  Illustration of quasi-fractonic hopping on a torus, and of anyon count via the mixed volume (purple parallelogram) of Newton polytopes (red and green triangles) specified by interacting qubits’ relative positions.

These results illuminate the intrinsic connections among quantum error correction, anyon excitations, symmetries, and topological phases of matter, providing crucial theoretical tools for the development of next-generation high-performance QEC codes. Building on these principles, team members further extended BB codes to twisted periodic boundary conditions in a related concurrent work published in PRX Quantum [6], achieving an additional improvement in error-correction efficiency.

The research was supported by the National Natural Science Foundation of China, the Chinese Academy of Sciences, the Anhui Initiative in Quantum Information Technologies, the Shanghai Municipal Science and Technology Major Project, and Peking University.

References:
[1] Sergey Bravyi, Andrew W. Cross, Jay M. Gambetta, Dmitri Maslov, Patrick Rall & Theodore J. Yoder, “High-threshold and low-overhead fault-tolerant quantum memory,” Nature 627, 778–782 (2024).

[2] Keyang Chen, Yuanting Liu, Yiming Zhang, Zijian Liang, Yu-An Chen, Ke Liu, & Hao Song, “Anyon Theory and Topological Frustration of High-Efficiency Quantum Low-Density Parity-Check Codes,” Phys. Rev. Lett. 135, 076603 (2025).

[3] Sagar Vijay, Jeongwan Haah, & Liang Fu, “Fracton topological order, generalized lattice gauge theory and duality,” Phys. Rev. B 94, 235157 (2016).

[4] Hao Song, Nathanan Tantivasadakarn, Wilbur Shirley, & Michael Hermele, “Fracton Self-Statistics,” Phys. Rev. Lett. 132, 016604 (2024).

[5] Jeongwan Haah, “Commuting Pauli hamiltonians as maps between free modules,” Commun. Math. Phys. 324, 351–399 (2013).

[6] Zijian Liang, Ke Liu, Hao Song, & Yu-An Chen, “Generalized Toric Codes on Twisted Tori for Quantum Error Correction,” PRX Quantum 6, 020357 (2025).

Link:

https://doi.org/10.1103/86j7-cmsw

Contact:

Hao Song

Email: songhao@itp.ac.cn

Institute of Theoretical Physics, CAS