One of the central challenges in cosmology is to understand how primordial perturbations evolve from quantum fluctuations into the macroscopic structures observed in today’s universe. Within the inflationary paradigm, the curvature perturbation ζ originates from quantum fluctuations of the inflaton field. Once stretched beyond the Hubble horizon, ζ approaches a constant value, which later reenters the horizon during the radiation-dominated era and determines the temperature fluctuations of the cosmic microwave background and the matter density distribution across the universe. In regions where ζ is sufficiently large, the gravitational collapse can lead to spacetime singularities with densities so high that even light cannot escape—these are known as primordial black holes. Such objects are a major focus of current research in cosmology and astrophysics, as they may constitute a significant fraction of dark matter.

For many years, the so-called δN formalism has been widely used to study the nonlinear evolution of ζ in various inflationary models. This method relies on the separate universe approach: on super-Hubble scales, spatial gradients decay rapidly, and each Hubble patch (the “cosmos” referred to in the title) evolves independently as a spatially flat Friedmann universe. δN formalism tells us that, in this picture, the curvature perturbation in each patch is given by the deviation of the local expansion from the background, ζ = δN, where δN is a function of the inflaton field value at horizon crossing, thus is a random variable among all the patches. Originally developed by Sasaki and collaborators, this formalism has become a cornerstone of early-universe cosmology due to its clear physical interpretation and computational simplicity [1–3].

However, recent work has shown that the standard δN formalism may break down in certain inflationary models, particularly when the inflaton enters an ultra-slow-roll phase. In such non-attractor regimes, perturbations continue to evolve after horizon exit, and spatial gradients cannot be neglected for more than a few Hubble times. This invalidates the separate universe approach and makes the δN formalism inapplicable unless one waits for gradients to decay. In such cases, one must resort to solving the full nonlinear evolution numerically, losing the key advantage of δN [4].

To overcome this limitation, Professor Shi Pi of the Institute of Theoretical Physics, Chinese Academy of Sciences, in collaboration with Dr. Danilo Artigas and Professor Takahiro Tanaka of Kyoto University, has developed an extended δN formalism. This approach introduces the spatial curvature K of each Hubble patch as an additional initial condition in the δN formalism. By delibertately choosing the gauge on the initial hypersurface, the gradient of the inflaton field can be absorbed into the spatial curvature, allowing the method to retain information about superhorizon evolution. As a result, this extended formalism can track ζ continuously from horizon exit moment—without waiting for the decay of gradient terms.

The method is demonstrated using the Starobinsky’s linear potential model as an example. Detailed analytical derivation and numerical calculation show that the extended δN formalism significantly improves both accuracy and computational efficiency over the traditional approach (see Fig. 1 for details). Moreover, it naturally facilitates the calculation of non-Gaussianities. For instance, in the ultra-slow-roll case, the nonlinearity parameter is 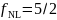, consistent with the logarithmic duality proposed by Shi Pi and Misao Sasaki in 2023 [5]. This implies that the extended δN formalism can directly be used to compute the probability distribution of ζ and the abundance of primordial black holes, providing a more reliable theoretical tool for related studies.

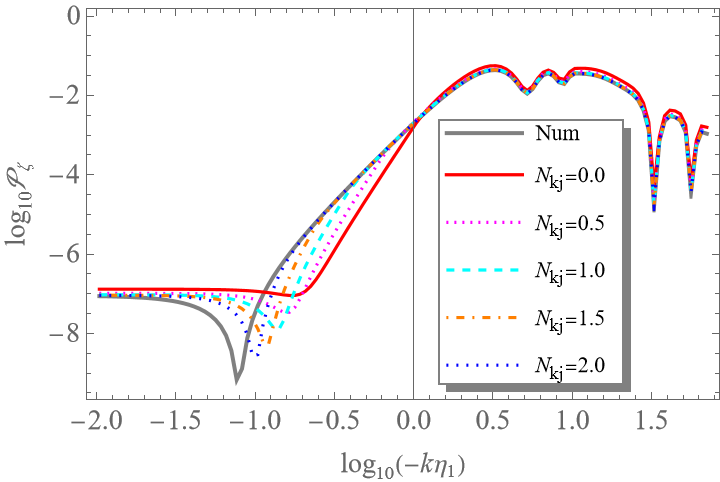
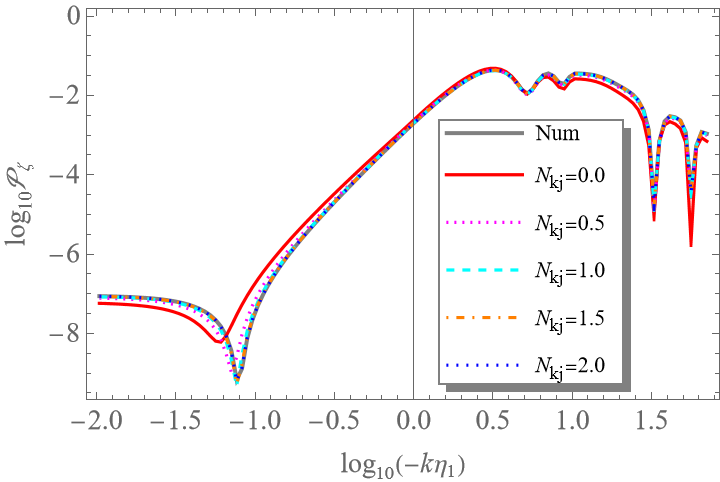
Fig.1 The power spectrum of the curvature perturbation ζ calculated using the δN formalism (left) and the extended δN formalism (right) for the Starobinsky model. It can be seen that the standard δN formalism becomes valid only several Hubble times after horizon exit, while the extended formalism yields accurate results immediately. The remaining small deviation arises from higher-order terms in spatial curvature and is negligible.

Reflecting on the broader implications, Shi Pi commented: “We hope this work lays the foundation for a more universal framework to describe nonlinear perturbation dynamics in more complicated backgrounds. While the δN formalism is a classical tool, its use has been confined to attractor phases. This extension marks a critical upgrade, with great potential for further applications—particularly in the study of primordial black holes and the induced stochastic gravitational wave background.”

This research is published in Physical Review Letters under the title “Extended δN Formalism: Separate Universe Approach with Spatial Curvature”. Danilo Artigas, Shi Pi, and Takahiro Tanaka are joint corresponding authors. The project was supported by the National Key R&D Program of China, the National High-Level Talent Special Support Program (Youth Project), the National Natural Science Foundation of China, T.D. Lee Youth Scholar Program of Center for High Energy Physics of Peking University, and the Japan Society for the Promotion of Science.

Original paper:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.221001

References:

1. M. Sasaki and E.D. Stewart, Prog. Theor. Phys.95, 71 (1996) [astro-ph/9507001].
2. M. Sasaki and T. Tanaka, Prog. Theor. Phys.99, 763 (1998) [gr-qc/9801017].
3. D.H. Lyth, K.A. Malik, M. Sasaki, JCAP0505, 004 (2005) [astro-ph/0411220].
4. J. Jackson et al., JCAP05, 053 (2024) [astro-ph.CO/2311.03281].
5. S. Pi and M. Sasaki, Phys. Rev. Lett.131, 011002 (2023) [astro-ph.CO/2211.13932].