Research Progress
Jamming transition: a first-order phase transition in disordered systems
The liquid-to-crystal transition, such as water freezing into ice, is generally a first-order phase transition. What is the nature of the phase transition between a liquid and an amorphous solid? The research group led by Dr. Yuliang Jin at the Institute of Theoretical Physics, Chinese Academy of Sciences, has discovered that the first-order phase transitions between liquids and amorphous solids exhibit different scaling behavior from ordinary liquid-solid phase transitions, through studies of the jamming transition. Their research shows that the jamming transition, under athermal and quasi-static loading conditions, should be classified as a "first-order phase transition with quenched disorder". The research findings were recently published in Nature Communications (https://www.nature.com/articles/s41467-024-51319-4).
Many soft-matter systems, such as granular materials, foams, emulsions, and cells, display a jamming transition between a flow state and an amorphous solid state. The configurations are disordered before and after the jamming transition, and the system is thermodynamically out-of-equilibrium. These features are accompanied with several mysterious properties near the jamming transition. For example, the jamming transition seems to exhibit characteristics of both first- and second-order transitions. The former is suggested by a discontinuity of the average contact number per particle (an order parameter) at the transition, and the latter is supported by diverging length scales near the transition.
This study shows that the jamming transition is a first-order phase transition with quenched disorder under two conditions. The first condition is that fluctuations due to disorder should dominate over thermal fluctuations, and the second is that the external loading, such as shear and compression, should be applied quasi-statically. The quenched disorder plays an important role in the behavior of the jamming transition. For example, violating the fluctuation-dissipation relation, the disconnected susceptibility χ_dis defined from fluctuations and the connected susceptibility χ_con defined from responses are not equal but instead follow a quadratic relationship (Figure 1). In addition to the jamming transition, several other phase transitions in disordered systems also fall into the category of first-order phase transitions with quenched disorder, including the first-order phase transition in the random field Ising model, the brittle yielding of amorphous solids, and the melting of ultra-stable glasses.
This work was financially supported by the National Natural Science Foundation of China, the Chinese Academy of Sciences, and the Wenzhou Institute of the Chinese Academy of Sciences. It was also granted access to the High-Performance Computing Platform of the Institute of Theoretical Physics, Chinese Academy of Sciences.
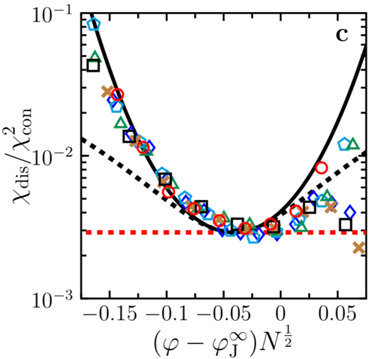
Figure 1:The disconnected susceptibility χ_dis and the connected susceptibility χ_con satisfy a quadratic relationship at the jamming transition.
