How the quark and gluon form the nucleon is one of the central questions in the particle physics research. Based on the existed collider experiments at high energy, the parton structure of nucleon along the longitudinal direction becomes quite clear, and the first principle Lattice quantum chromodynamics (LQCD) calculation can also provide more and more accurate prediction for the parton distribution function (PDF). But predicting the Drell-Yan and Semi-inclusive deep inelastic scattering also requires the transverse momentum dependent PDF of nucleon, which is not only one of the major goals of the proposed electron-ion colliders in China and USA, and also a critical challenge on the LQCD prediction capability. 

At the same time, the light pseudo-scalar meson being the pseudo-Goldstone boson generated by the spontaneous chiral symmetry breaking, plays a crucial role in the low energy effective theory of QCD. Its structure and impact on the experimental always receives many attentions. Among the describes how the momentum of quark and anti-quark in the pseudoscalar mesons is distributed in the direction of meson motion. Therefore, it is an important theoretical input in terms of B meson weak decay, pion elastic form factor and pion-photon transition form factor, and also nucleon generalized distribution function. 

However, in the definitions of PDF and LCDA which use the similar operator, the Wilson line along the light cone is included. Even more, the definition of TMDPDF includes the Wilson line that extends to infinity and then turns back in the direction of the light cone. Therefore, they cannot be directly calculated using the LQCD which is defined in the Euclidean space. The Large Momentum Effective Theory (LaMET) regards the physics on the light-cone as an effective theory of high-speed moving particles. By introducing the spatial direction Wilson lines to replace these incalculable light-cone Wilson lines, the quasi light-cone matrix elements that can be calculated by LQCD is introduced. Then we can get predictions of PDF, LCDA and TMDPDF, through perturbative LaMET matching. However, in the LQCD, Wilson lines in the spatial direction have UV divergence that increases exponentially with the Wilson line length, and for the infinite long Wilson lines required by quasi-TMD, this divergence tends to infinity. Thus all those divergences need to be accurately eliminated by non-perturbative renormalization. 

The most common method of non-perturbative renormalization is the regularization independent momentum subtraction scheme (RI/MOM). In this renormalization scheme, the off-shell quark matrix elements with spacelike momentum, are used as transients to connect the Lattice and dimensional regularizations. As the ultraviolet divergence should be independent of the external state, this scheme can be used to obtain the renormalization constant of the hadron matrix elements. Since it was proposed in 1994, the RI/MOM scheme has been widely applied to the renormalization of local operators, and was applied to the renormalization of quasi PDF in 2017 [1]. The calculation results of Ref. [1] show that when the lattice spacing is about 0.1fm, the MOM scheme can effectively eliminate the exponential divergence of the hadron quasi PDF matrix element under lattice regularization by dividing the off shell quark matrix element, and make the theoretical prediction to be agree with the experiments. But when the lattice spacing becomes smaller, the statistical uncertainty increases exponentially and then one can not judge accurately on whether the exponential divergence is fully eliminated. 

Therefore, the Lattice Group of ITP-CAS and their colleagues of the χQCD collaboration proposed a scheme to examine the pion quasi-PDF matrix elements in the rest frame for the effectiveness of RI/MOM scheme [2]. Compared with the nucleon calculation in the moving frame, the signal-to-noise ratio of the pion matrix element in the rest frame can be improved by a factor of thousands, which allows an accurate test on whether the exponential divergence is completely eliminated in a wider lattice spacing and Wilson link length range. The accurate results on 11 lattice spacings from 0.03fm to 0.12fm show that the residual divergence in the RI/MOM renormalized quasi-PDF hadronic matrix elements has been much smaller than that in the original bare matrix elements, which suggests that the exponential divergence is indeed eliminated at the leading order or equivalently one loop level; However, as shown in Fig. 1, the quark matrix element used in the RI/MOM scheme has some residual exponential divergence which is sensitive to the quark discretization scheme (which would be gauge dependent) at two loop level, thus it can not completely eliminate all the exponential divergence in the hadron matrix element [2].

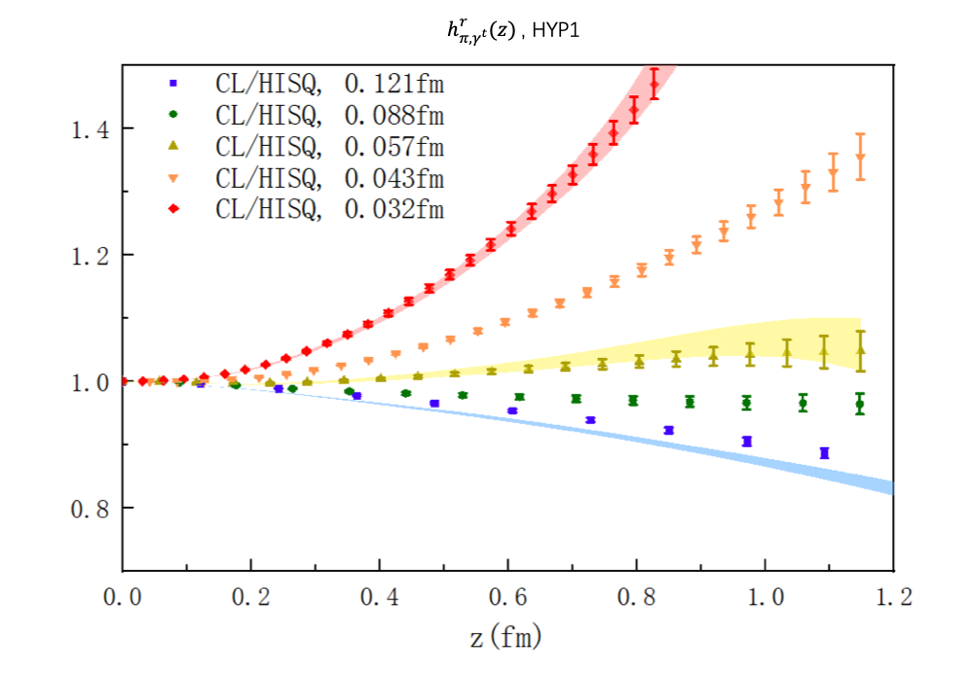
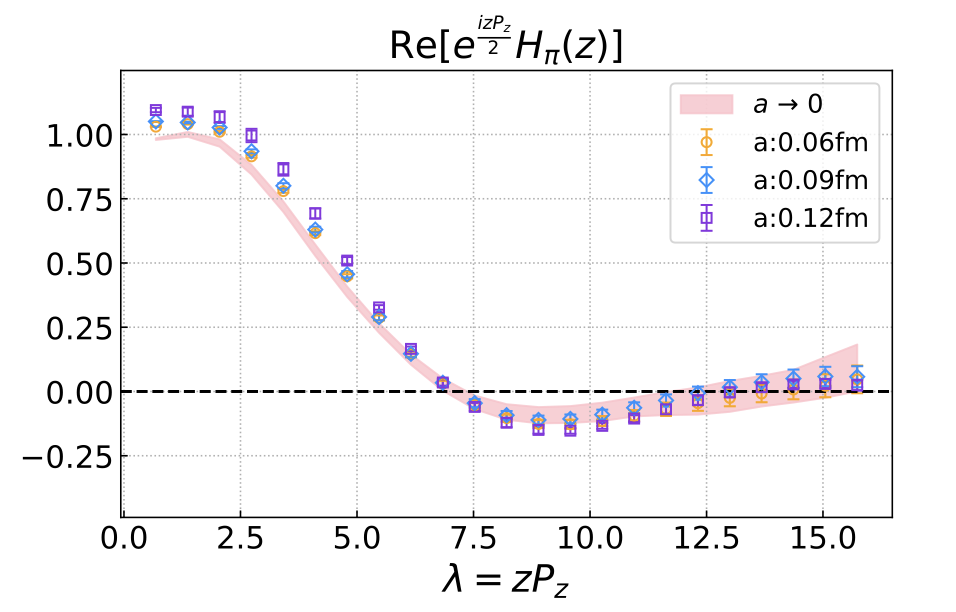
Fig. 2: The quasi-LCDA matrix elements and their continuum limits (red band) at different lattice spacings with the self-renormalization scheme. Compared with the momentum subtraction scheme, the self-renormalization scheme completely eliminates the linear divergence and then has a well-defined continuum limit.

Fig. 3: The LQCD prediction (yellow band) extrapolated to the continuum and infinite momentum limits based on LaMET, for the LCDA of pion (left panel) and kaon(right panel). Different from the pion case, the kaon LCDA has obvious asymmetry on x. For the hadron momentum used in the current calculation, the intrinsic energy scale in the regions x<0.1 and x>0.9 is too low to give reliable predictions through LaMET, and then shadowed by the grey bands. 

Further more, LPC investigated the quasi-TMD case, and find the problem of RI/MOM scheme is similar to the quasi-PDF case [6]. As shown in Fig. 4, when the momentum subtraction scheme is used for renormalization, the quasi-TMD matrix elements with different lattice spacing (marked by different colors) becomes far away from each other when the lattice spacing is smaller, and then do not converge when the lattice spacing approaches zero. However, if we combine the square root of Wilson loop with the short distance quasi-TMD hadron matrix element, we can effectively eliminate all UV divergence of the quasi-TMD operator, and make the results at different lattice spacings to be consistent with each other and also the analytical calculation results at the short distance, as illustrated in Fig. 4. The paper was published in Phys. Rev. Lett. at August [6].

Fig. 4: The renormalized quasi-TMD matrix elements using the momentum subtraction scheme (left panel) and the short-range subtraction scheme (right panel). Different colors represent different lattice spacing, and a warmer color corresponds to a smaller lattice spacing. As shown in the figure, the matrix element using momentum subtraction scheme cannot converge when the lattice spcing approaches 0; But the short-range subtraction scheme can obtain the convergent results which are exactly consistent with the analytical calculation (dotted line) at the short-distance. 

At the same time, combining the data in Fig. 1 and 4, one can see that the residual divergences of quasi-PDF and quasi-TMD matrix elements under the RI/MOM scheme are almost identical, which only depends the distance of the quark and anti-quark along in the hadron momentum direction, but not the distance in the transverse direction. This fact would be instructive for further unifying the renormalization scheme of quasi-PDF and quasi-TMD matrix elements in the future. 

LPC was established in 2019, including researchers from the ITP-CAS, IMP-CAS, Shanghai Jiaotong University, Beijing Normal University, Nanjing Normal University, Hunan University, Hunan Normal University, South China Normal University, University of Maryland (in US) and University of Regensburg (in Germany). LPC concentrates on the LQCD hadronic structure study based on the domestic LQCD researchers and supercomputing resources. Yi-Bo Yang served as the spokesperson of the LPC, and provided architecture and scheme design, as well as numerical calculation training for LPC. Since its establishment, LPC has published seven articles, including four Phys. Rev. Lett [4,5,6,7], two Phys. Rev. D [8,9], and one Nuc. Phys. B [3]. 

Jun Hua as an associate researcher of South China Normal University, is the first author of the pseudo-scalar meson LCDA work; and Kuan Zhang as an doctoral student of ITP-CAS, is the first author of the TMD renormalization work. The co-corresponding authors of the two papers are Yi-Bo Yang from ITP-CAS, and Jian-Hui Zhang from Beijing Normal University. The numerical calculation of this research is mainly based on the ORISE supercomputer of CAS, and the advanced computing platform of IPT. The research work is supported by the Strategic Priority Research Program of Chinese Academy of Sciences, National Natural Science Foundation of China grants, NSFC-DFG joint grants and also Natural Science Foundation of Shanghai. 

[1] J. Chen, et al., LP3, PRD97(2018) 014507

[2] K. Zhang, et al.,χ QCD, PRD104(2021) 074501;

[3] Y. Huo, et.al., LPC NPB969(2021) 115443;

[4] J. Hua, et al., LPC, PRL129(2022) 132001;

link：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.132001

[5] J. Hua, et al., LPC, PRL127(2021) 062002;

[6] K. Zhang, et al., LPC, PRL119(2022) 082002,

link：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.082002

[7] Q. Zhang, et al., LPC, PRL125(2020) 192001;

[8] Y. Liu, et al., LPC, PRD101(2020) 034020;

[9] M. Chu, et al., PRD106(2022) 034509.